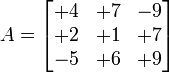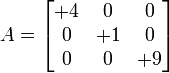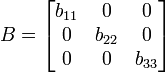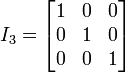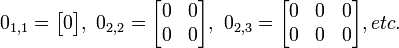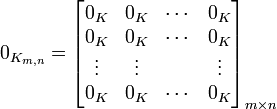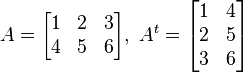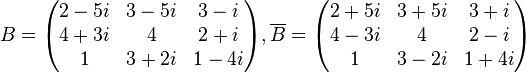MODULO 4. SISTEMAS DE ECUACIONES LINEALES Y MATRICES.
Objetivo.
El alumno entenderá los conceptos elementales del álgebra lineal y los aplicara en problemas del ámbito económico y de negocios.
4.1 sistema de ecuaciones lineales.
un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde  son las incógnitas y los números
son las incógnitas y los números 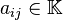 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
 son las incógnitas y los números
son las incógnitas y los números 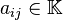 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
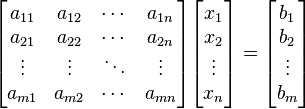
Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este sistema lineal. A b se le llama vector de términos independientes del sistema y a x se le llama vector de incógnitas.
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Julio profe. (2012). Sistema de Ecuaciones Lineales 2x2 por Método Gráfico . Noviembre30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=ieiRIATCOUI
4.1.1 definición.
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o unanillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como enprocesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
4.1.2 sistema de ecuaciones lineales: consistente, inconsistente, y su representación paramétrica del conjunto solución.
Un sistema de ecuaciones lineales sin solución, se denomina sistema de ecuaciones inconsistente. Un sistema de ecuaciones lineales con única solución, se denomina sistema de ecuaciones consistente con única solución y un sistema de ecuaciones lineales con infinitas soluciones, se denomina sistema de ecuaciones consistente con infinitas soluciones.
Ejemplos:
Desarrollar el siguiente sistema de ecuaciones:
Sistema de ecuaciones inconsistente.
Desarrollar el siguiente sistema de ecuaciones:
Sistema de ecuaciones consistente con única solución.
Desarrollar el siguiente sistema de ecuaciones:
Sistema de ecuaciones consistente con infinitas soluciones.
EL ESPACIO VECTORIAL Rn
Un espacio vectorial es un conjunto de vectores Rn, las cuales se pueden graficar en un plano:
También pueden unirse los puntos mediante una recta. (-1,-1,-1)(0,0,0)(2,2,2)



Para hacer un grafico en R2 o en R3, podemos optar por graficar como:
Punto.
Una flecha que parta del origen.
Una flecha que parta de un punto distinto al origen.
http://html.rincondelvago.com/algebra-lineal_4.html
Carlos Mejia. (1998). Álgebra lineal. 2015, de andrea Sitio web: http://html.rincondelvago.com/algebra-lineal_4.html
4.1.3 métodos para resolución de sistemas de ecuaciones lineales: metodo grafico, igualacion, sustitucion, eliminacion (sumas y restas).
Sistemas lineales reales
En esta sección se analizan las propiedades de los sistemas de ecuaciones lineales sobre el cuerpo  , es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
 , es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.
, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son números reales.Representación gráfica
Un sistema con  incógnitas se puede representar en el n-espacio correspondiente.
incógnitas se puede representar en el n-espacio correspondiente.
 incógnitas se puede representar en el n-espacio correspondiente.
incógnitas se puede representar en el n-espacio correspondiente.
En los sistemas con 2 incógnitas, el universo de nuestro sistema será el plano bidimensional, mientras que cada una de lasecuaciones será representada por una recta. La solución será el punto (o línea) donde se intersequen todas las rectas representan a las ecuaciones. Si no existe ningún punto en el que se intersequen al mismo tiempo todas las líneas, el sistema es incompatible, o lo que es lo mismo, no tiene solución.
En el caso de un sistema con 3 incógnitas, el universo será el espacio tridimensional, siendo cada ecuación un plano dentro del mismo. Si todos los planos intersecan en un único punto, las coordenadas de este serán la solución al sistema. Si, por el contrario, la intersección de todos ellos es una recta o incluso un plano, el sistema tendrá infinitas soluciones, que serán las coordenadas de los puntos que forman dicha línea o superficie.
Para sistemas de 4 o más incógnitas, la representación gráfica no existe, por lo que dichos problemas no se enfocan desde esta óptica.
Métodos de solución a sistemas de ecuaciones lineales
Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones con cualquier incógnita, preferiblemente la que tenga menor coeficiente y a continuación sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita  por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita  en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
Al resolver la ecuación obtenemos el resultado 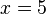 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 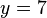 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.
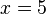 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 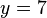 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.Igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita  en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita  , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
 , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Reducción
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, medianteproductos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.
Por ejemplo, en el sistema:
No tenemos más que multiplicar la primera ecuación por 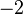 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
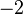 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
Si sumamos esta ecuación a la segunda del sistema original, obtenemos una nueva ecuación donde la incógnita  ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
 ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
El siguiente paso consiste únicamente en sustituir el valor de la incógnita  en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:
 en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:Método gráfico
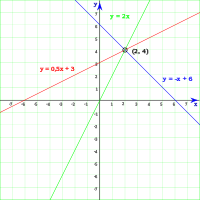
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión .
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:
- Se despeja la incógnita en ambas ecuaciones.
- Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
- Se representan gráficamente ambas rectas en los ejes coordenados.
- En este último paso hay tres posibilidades:
- Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".
- Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
- Si ambas rectas son paralelas, el sistema no tiene solución en los reales pero si en los complejos.
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
4.1.4 sistemas de ecuaciones equivalentes.
Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
- Sistema compatible si tiene solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene una única solución.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.
- Sistema incompatible si no tiene solución.
Quedando así la clasificación:
Los sistemas incompatibles geométricamente se caracterizan por (hiper)planos o rectas que se cruzan sin cortarse. Los sistemas compatibles determinados se caracterizan por un conjunto de (hiper)planos o rectas que se cortan en un único punto. Los sistemas compatibles indeterminados se caracterizan por (hiper)planos que se cortan a lo largo de una recta [o más generalmente un hiperplano de dimensión menor]. Desde un punto de vista algebraico los sistemas compatibles determinados se caracterizan porque el determinante de la matriz es diferente de cero:
Algoritmo para determinar si un sistema es compatible
Podemos averiguar si un sistema es o no compatible mediante el Teorema de Rouché-Frobenius que establece que un sistema de ecuaciones lineales es compatible sólo si el rango de su matriz ampliada coincide con el de su matriz de coeficientes. Supongamos que el sistema es compatible. Si el valor común de los rangos de las matrices coincide con el número de variables, el sistema es compatible determinado; en caso contrario, es compatible indeterminado.
Sistemas compatibles indeterminados[editar]
Un sistema sobre un cuerpo K es compatible indeterminado cuando posee un número infinito de soluciones. Por ejemplo, el siguiente sistema:
Tanto la primera como la segunda ecuación se corresponden con la recta cuya pendiente es  y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
 y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.- En este tipo de sistemas, la solución genérica consiste en expresar una o más variables como función matemática del resto. En los sistemas lineales compatibles indeterminados, al menos una de sus ecuaciones se puede hallar como combinación lineal del resto, es decir, es linealmente dependiente.
- La condición necesaria para que un sistema sea compatible indeterminado es que el determinante de la matriz del sistema sea cero al igual que el rango de la matriz ampliada y menor al número de incógnitas(y por tanto uno de sus autovalores será 0):
- De hecho, de las dos condiciones anteriores se desprende, que el conjunto de soluciones de un sistema compatible indeterminado es un subespacio vectorial. Y la dimensión de ese espacio vectorial coincidirá con la multiplicidad geométrica del autovalor cero.
Sistemas incompatibles[editar]
De un sistema se dice que es incompatible cuando no presenta ninguna solución. Por ejemplo, supongamos el siguiente sistema:
Las ecuaciones se corresponden gráficamente con dos rectas, ambas con la misma pendiente, Al ser paralelas, no se cortan en ningún punto, es decir, no existe ningún valor que satisfaga a la vez ambas ecuaciones.
Matemáticamente un sistema de estos es incompatible cuando el rango de la matriz del sistema es inferior al rango de la matriz ampliada. Una condición necesaria para que esto suceda es que el determinante de la matriz del sistema sea cero:
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
UnProfesor. (2014). Criterios de equivalencia de los sistemas de ecuaciones . noviembre30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=Xrwov-fwi-8
4.1.5 eliminacion de Gauss y Gauss-jordan.
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
Una variante de este método, denominada eliminación de Gauss-Jordan, es un método aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en triangular la matriz aumentada del sistema mediante transformaciones elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será igual al coeficiente situado en la misma fila de la matriz. Este procedimiento es similar al anterior de reducción, pero ejecutado de manera reiterada y siguiendo un cierto orden algorítmico.Eliminación de Gauss-Jordan
Regla de CramerRegla de Cramer
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
Fundación Wikimedia, Inc.. (2015). Sistema de ecuaciones lineales. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales#Sistemas_lineales_reales
4.1.5.1 definición de matriz.
Se puede definir una matriz, como un conjunto de elementos (números) ordenados en filas y columnas.
| Para designar una matriz se emplean letras mayúsculas. Cada uno de los elementos de la matriz (aij) tiene dos subíndices. El primero i indica la fila a la que pertenece y el segundo j la columna. Esta es una matriz de m filas y n columnas, es decir, de dimensión m x n. Esta matriz también se puede representar de la forma siguiente: A = (aij) m x n. Si el número de filas y de columnas es igual ( m = n ), entonces se dice que la matriz es de orden n. http://recursostic.educacion.es/descartes/web/materiales_didacticos/matrices/matrices_definicion_y_tipos.htm Ministerio de Educación, Cultura y Deporte. (2006). MATRICES: DEFINICIÓN Y TIPOS. 2015, de andrea Sitio web: http://recursostic.educacion.es/descartes/web/materiales_didacticos/matrices/matrices_definicion_y_tipos.htm https://www.youtube.com/watch?v=AIoa_aTOrh8
4.1.5.2 expresion matricial de un sistema de ecuaciones lineales.Dado un sistema de ecuaciones |
http://www.vitutor.com/algebra/sistemas%20I/homogeneos_2.html
https://www.youtube.com/watch?v=gfWR1vv8LM0
@vitutor 2014. (2014). Sistemas homogéneos. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/sistemas%20I/homogeneos_2.html
https://www.youtube.com/watch?v=gfWR1vv8LM0
Educatina. (2014). Sistemas Homogeneos. noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=gfWR1vv8LM0
4.2 Álgebra de matrices.
La matriz unidad de orden n×n es la matriz I de orden n×n en la cual todas las entradas son cero excepto los de la diagonal principal, que son 1. En símbolos:
- Iij = 1 si i = j y Iij = 0 si i ≠ j.
Una matriz cero es una matriz O en la cual todas las entradas son cero.
Las operaciones de adición, multiplicación escalar, multiplicación entre matrices se cumplen las siguientes reglas:
| A+(B+C) = (A+B)+C | Regla asociativa de adición |
| A+B = B+A | Regla conmutativa de adición |
| A+O = O+A = A | Regla unidad de adición |
| A+( - A) = O = ( - A)+A | Regla inversa de adición |
| c(A+B) = cA+cB | Regla distributiva |
| (c+d)A = cA+dA | Regla distributiva |
| 1A = A | Unidad escalar |
| 0A = O | Cero escalar |
| A(BC) = (AB)C | Regla asociativa de multiplicación |
| AI = IA = A | Regla unidad de multiplicación |
| A(B+C) = AB + AC | Regla distributiva |
| (A+B)C = AC + BC | Regla distributiva |
| OA = AO = O | Multiplicación por matriz cero |
| (A+B)T = AT + BT | Trasposición de una suma |
| (cA)T = c(AT) | Trasposición de un producto escalar |
| (AB)T = BTAT | Trasposición de un producto matriz |
La única regla que está notablemente ausente es la de conmutatividad del producto entre matrices. El producto entre matrices no es conmutativo: AB no es igual a BA en general.
http://www.zweigmedia.com/MundoReal/Summary3a.html
Stefan Waner . (2007). Matemáticas finitas resumen del tema: álgebra de matrices. 2015, de andrea Sitio web: http://www.zweigmedia.com/MundoReal/Summary3a.html
4.2.1 tipos de matrices (cuadrada, rectangular triangular, matriz identidad, matriz transpuesta).
Matríz cuadrada
Se dice que una matriz A es cuadrada si tiene el mismo número de filas que de columnas. Ejemplos de matriz cuadrada:
Puede ser una matriz con valores 

O también una matríz con subíndices (Genérica)

Puede ser de otro tamaño e incluso con variables 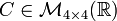
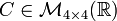
Se llama diagonal principal de una matriz A a la diagonal formada por los elementos 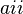 .
.
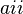 .
.
Se llama diagonal secundaria a la diagonal del cuadrado que no es la principal, tiene por extremos los elementos  y
y 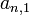 , como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo  , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.
 y
y 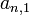 , como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo  , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.Matriz Rectangular
Es aquella matriz que no es cuadrada, esto es que la cantidad de filas es diferente de la cantidad de columnas.
Puede ser de dos formas; vertical u horizontal.
Matriz Vertical
Es aquella que tiene más filas que columnas.
Matriz Columna
Caso especial de matriz vertical que posee una sola columna.
Matriz Horizontal
Es aquella que tiene más columnas que filas.
Matriz Fila
Caso especial de matriz horizontal que posee una sola fila.
Matriz Diagonal
Se llama diagonal principal de una matriz A a la diagonal formada por los elementos aij.
Matriz diagonal, matriz cuadrada donde sus elementos 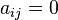 si
si 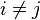 .
.
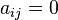 si
si 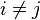 .
.
La matriz identidad es una matriz diagonal.
Una matriz diagonal es una matriz cuadrada en que las entradas o valores son todos nulas salvo en la diagonal principal, y éstos incluso pueden ser nulos o no. Otra forma de decirlo es que es diagonal si todos sus elementos son nulos salvo algunos de la diagonal principal. Ejemplos de matrices Diagonales:
Puede ser una matriz con valores 

O también una matríz con subíndices (Genérica)

Puede ser de otro tamaño e incluso con variables 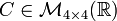
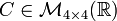
Matriz Escalonada
Es toda matriz en la que el número de ceros que precede al primer elemento no nulo, de cada fila o de cada columna, es mayor que el de la precedente.
Puede ser escalonada por filas o escalonada por columnas.
Matriz Triangular superior
Se dice que una matriz (cuadrada) es triangular superior si todos los elementos que están por debajo de la diagonal principal son nulos.
Matriz Triangular inferior
Se dice que una matriz es triangular inferior si todos los elementos que están por encima de la diagonal principal son ceros.
Matriz Identidad
Se llama matriz identidad de orden n y se nota In a una matriz cuadrada de orden n en la que los elementos de la diagonal principal son 1 y el resto 0.
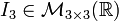
La matriz identidad puede ser de cualquier tamaño, siempre y cuando sea cuadrada
Matriz Nula o Matriz Cero
Una matriz cero o matriz nula es una matriz con todos sus elementos nulos, o sea de valor cero. Algunos ejemplos de matrices nulas son:
Por lo tanto, una matriz nula de orden mxn asume la forma:
Una matriz cero es, al mismo tiempo,matriz simétrica, antisimétrica, nilpotente y singular.
Matriz Opuesta
Teniendo una matriz determinada, se llama matriz opuesta de la antes mencionada a aquella que tiene por elementos los opuestos de los elementos de la matriz original.
Matriz Traspuesta
Matriz traspuesta (At). Se llama matriz traspuesta de una matriz A a aquella matriz cuyas filas coinciden con las columnas de A y las columnas coinciden con las filas de A.
- Para una matriz
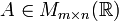 , se define la matriz transpuesta de
, se define la matriz transpuesta de  , denotada por
, denotada por 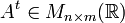 , como
, como 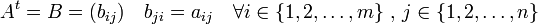 . Es decir, las filas de la matriz
. Es decir, las filas de la matriz  corresponden a las columnas de
corresponden a las columnas de  y viceversa.
y viceversa.
Matriz Simétrica
Una matriz es simétrica cuando es una matriz cuadrada, y es igual a su traspuesta.
Matriz Antisimétrica
Una matriz es antisimétrica cuando es una matriz cuadrada, y es igual a su traspuesta de signo opuesto, siendo los elementos de la diagonal principal nulos; de valor cero.
Matriz Ortogonal
Una matriz ortogonal es una matriz cuya matriz inversa coincide con su matriz traspuesta.
Matriz Normal
Sea A matriz compleja cuadrada, entonces es una matriz normal si y sólo si
donde A* es la matriz traspuesta conjugada de A (también llamado hermitiano)
Matriz Conjugada
Una Matriz conjugada es el resultado de la sustitución de los elementos de una matriz  por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
 por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
Ejemplo de matrices conjugadas
Matriz Invertible
También llamada matriz , no singular, no degenerada, regular.
Una matriz cuadrada A de orden n se dice que es invertible si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A−1, tal que
- AA−1 = A−1A = In,
donde In es la matriz identidad de orden n y el producto utilizado es el producto de matrices usual. Una matriz tiene inversa siempre que su determinante no sea cero.
La inversión de matrices es el proceso de encontrar la matriz inversa de una matriz dada.
Matriz Singular o Degenerada
También llamada no regular. Una matriz es singular si y solo si su determinante es cero.
Matriz Permutación
La matriz permutación es la matriz cuadrada con todos sus n×n elementos iguales a 0, excepto uno cualquiera por cada fila y columna, el cual debe ser igual a 1.
Matrices iguales
Se dice que dos matrices A y B son iguales si tienen la misma dimensión y son iguales elemento a elemento, es decir, aij=bij i=1,...,n j=1,2,...,m.
Matriz Hermitiana
Una matriz Hermitiana (o Hermítica) es una matriz cuadrada de elementos complejos que tiene la característica de ser igual a su propia traspuesta conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j.
Matriz definida positiva
Una matriz definida positiva es una matriz hermitiana que en muchos aspectos es similar a un número real positivo.
Matriz Unitaria
Es una matriz compleja U, de n por n elementos, que satisface la condición:
donde 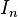 es la matriz identidad y
es la matriz identidad y  es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada
es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada  .
.
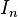 es la matriz identidad y
es la matriz identidad y  es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada
es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada  .
.
Una matriz unitaria en la que todas las entradas son reales es una matriz ortogonal.
Submatriz
A partir de una Matriz M, se llama submatriz M' a toda matriz obtenida suprimiendo p filas y q columnas en M. Si M es de orden mxn, M' será de orden (m-p)x(n-q), es decir con p filas menos y q columnas menos. Es evidente que p < m ; q < n.
https://es.wikibooks.org/wiki/Matem%C3%A1ticas/Matrices/Tipos_de_matrices
Creative Commons Atribución-CompartirIgual 3.0. (2015). Tipos de matrices. 2015, de andrea Sitio web: https://es.wikibooks.org/wiki/Matem%C3%A1ticas/Matrices/Tipos_de_matrices
4.2.2 operaciones con matrices.
Trasposición
La matriz traspuesta, AT, de la matriz A es la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A. Sea A una matiz m×n y B = AT, entonces B es la matriz n×m con bij = aji.
Suma, Resta
Sea A y B matrices con las mismas dimensiones, entonces sus suma, A+B, se obtiene sumando entradas correspondientes. En símbolos, (A+B)ij = Aij + Bij. En forma parecida, sus resta, A - B, obtiene restando entradas correspondientes. En símbolos, (A-B)ij = Aij - Bij.
Multiplicación escalar
Sea A una matriz y c un número (llamado un escalar en este contexto), definimos el múltiple escalar, cA, como la matriz que se obtiene multiplicando cada entrada de A por c. En símbolos, (cA)ij = c(Aij).
Producto
Sea A una matriz con dimensiones m×n y B una matriz con dimensiones n×p, entonces el producto AB está definido, y tiene dimenciones m×p. La entrada (AB)ij se obtiene por multiplicar reglón i de A por columna j de B, hecho por multiplicar sus entradas correspondientes y sumar las resultados.
http://www.zweigmedia.com/MundoReal/Summary3a.html
Stefan Waner . (2007). Matemáticas finitas resumen del tema: álgebra de matrices. 2015, de andrea Sitio web: http://www.zweigmedia.com/MundoReal/Summary3a.html
4.2.3 propiedades de las operaciones con matrices.
1. Interna
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
2. Asociativa
A + (B + C) = (A + B) + C
3. Elemento neutro
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
4. Elemento opuesto
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
5. Conmutativa
A + B = B + A
http://www.vitutor.com/algebra/matrices/operaciones.html
@vitutor 2014. (2014). Operaciones con matrices. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/matrices/operaciones.html
@vitutor 2014. (2014). Operaciones con matrices. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/matrices/operaciones.html
4.2.4 matriz inversa.
Si premultiplicamos (multiplicamos por la izquierda) o posmultiplicamos (multiplicamos por la derecha) una matriz cuadrada por su inversa obtenemos la matriz identidad.
A · A−1 = A−1 · A = I
Propiedades
1 (A · B)−1 = B−1 · A−1
2 (A−1)−1 = A
3 (k · A)−1 = k−1 · A−1
4 (At)−1 = (A−1)t
http://www.vitutor.com/algebra/matrices/inversa.html
@vitutor 2014. (2014). Matriz inversa. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/matrices/inversa.html
4.3 determinantes.
A cada matriz cuadrada A se le asocia un número denominado determinante de A.
El determinante de A se denota por |A| o por det (A).
A = 

Determinante de orden uno
|a 11| = a 11
|5| = 5
Determinante de orden dos
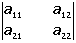 = a 11 a 22 - a 12 a 21
= a 11 a 22 - a 12 a 21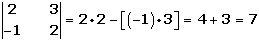
Determinante de orden tres
Consideremos una matriz 3 x 3 arbitraria A = (aij). El determinante de A se define como sigue:
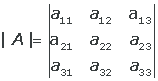 =
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
- a 13 a22 a31 - a12 a21 a 33 - a11 a23 a32.
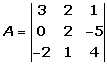 =
=
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 · 1 -
- 1 · 2 · (-2) - 2 · 0 · 4 - 3 · (-5) · 1 =
= 24 + 20 + 0 - (-4) - 0 - (-15) =
= 44 + 4 + 15 = 63
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz.Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo(cambian su signo).
http://www.ditutor.com/determinantes/determinante.html
@Ditutor 2015. (2015). Determinantes. 2015, de andrea Sitio web: http://www.ditutor.com/determinantes/determinante.html
4.3.1 definición de un determinante.
como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
https://es.wikipedia.org/wiki/Determinante_(matem%C3%A1tica)
Fundación Wikimedia, Inc.,. (2015). Determinante (matemática). 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Determinante_(matem%C3%A1tica)
Fundación Wikimedia, Inc.,. (2015). Determinante (matemática). 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Determinante_(matem%C3%A1tica)
4.3.2 expansionan por cofactores.
Expansión por cofactores de un determinante.
Se puede probar el siguiente
Teorema
Todo determinante es igual a la suma de los productos de los elementos de un renglón (o columna) cualquiera por sus cofactores correspondientes.
Esto es
 (2) (2)
es el desarrollo del determinante D por el renglón i, y similarmente
es el desarrollo del determinante D por la columna k.
|
Las expresiones (2) y (3) son fórmulas completamente generales, cualquier determinante de cualquier dimensión se puede evaluar usando estas fórmulas.
http://fcm.ens.uabc.mx/~matematicas/algebralineal/III%20Dets/menores%20y%20cofactores.htm
MENORES Y COFACTORES. (2014). MENORES Y COFACTORES. 2015, de andrea Sitio web: http://fcm.ens.uabc.mx/~matematicas/algebralineal/III%20Dets/menores%20y%20cofactores.htm
4.3.3 propiedades de los determinantes.
1 |At|= |A|
El determinante de una matriz A y el de su traspuesta At son iguales.


2 |A| = 0 Si:
Posee dos filas (o columnas) iguales.

Todos los elementos de una fila (o una columna) son nulos.

Los elementos de una fila (o una columna) son combinación lineal de las otras.

F3 = F1 + F2
3 Un determinante triangular es igual al producto de los elementos de la diagonal principal.

4 Si en un determinante se cambian entre sí dos filas (o dos columnas), su valor sólo cambia de signo.


5 Si a los elementos de una fila (o una columna) se le suman los elementos de otra multiplicados previamente por un número real, el valor del determinante no varía.
Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.


6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier fila (o cualquier columna), pero sólo una.

7 Si todos los elementos de una fila (o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas (o columnas) permanecen invariantes.

8 |A · B| =|A| · |B|
El determinante de un producto es igual al producto de los determinantes.
http://www.vitutor.com/algebra/determinantes/propiedades.html
@vitutor 2014. (2014). Propiedades de los determinantes. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/determinantes/propiedades.html
4.3.4 regla de Cramer.
La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:
1 El número de ecuaciones es igual al número de incógnitas.
2 El determinante de la matriz de los coeficientes es distinto de cero.
Tales sistemas son sistemas compatibles determinados y se denominan sistemas de Cramer.

Sea Δ el determinante de la matriz de coeficientes.

Todo sistema de Cramer tiene una sola solución (es decir, es un sistema compatible determinado) que viene dada por las siguientes expresiones:

Δ1, Δ2 , Δ3, ... , Δn son los determinantes que se obtiene al sustituir los coeficientes del 2º miembro (los términos independientes) en la 1ª columna, en la 2ª columna, en la 3ª columna y en la enésima columna respectivamente.



...

http://www.vitutor.com/algebra/sistemas%20I/cramer.html
@vitutor 2014. (2014). Regla de Cramer. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/sistemas%20I/cramer.html
@vitutor 2014. (2014). Regla de Cramer. 2015, de andrea Sitio web: http://www.vitutor.com/algebra/sistemas%20I/cramer.html
4.4 aplicaciones: modelo insumo-producto, análisis de ventas y comportamiento del consumidor.
En esta ocasión, este documento está dedicado a la explicación general del modelo Insumo-Producto desarrollado por Leontief, el cual se dedica a la descripción interindustrial e intersectorial existente de una economía capitalista principalmente.Como objetivo de la lectura, se plantea que el lector pueda comprender de una forma sencilla el modelo insumo producto a través de la explicación breve de sus principales componentes y de las principales matrices utilizadas.
El Modelo Insumo Producto (MIP) puede definirse como un método de análisis, utilizado tanto en economía teórica como aplicada, que tiene por objeto encontrar las relaciones entre los diferentes factores de producción utilizados y el producto que se obtiene de ellos. El análisis de insumo-producto no tiene en cuenta la demanda; su objetivo es determinar el nivel de eficiencia para un conjunto finito de factores con el propósito de producir un conjunto previamente determinado de bienes (Clark, 1964). Para llegar a este objetivo se considera un conjunto de ecuaciones lineales relacionadas entre sí cuya solución se obtiene mediante técnicas de programación lineal.
https://es.wikipedia.org/wiki/Comportamiento_del_consumidor
Jagdish C. Arya. (2009). Matemáticas aplicadas a la administración y a la economía. cuarta edición. México: PEARSON EDUCACION.
En este último modulo vimos cómo
hacer los sistemas de ecuaciones y sus diferentes formas de resolverlo como por
el meto de suma y resta, método de igualación, por sustitución, determinante.
Y en cada de uno de estos se tenían
que realizar operaciones diferentes y que a fin de cuentas en todas tiene que
darte el mismo resultado.
El álgebra matricial, vimos cómo
hacer sumas, restas, multiplicaciones, y cuáles eran las condiciones para
resolverlas y los diferentes pasos para cada operación; cuando comenzamos a
entender más esto empezamos a realizar ejercicios en los cuales te decía la información
que tenías que utilizar para resolverlo en forma de matriz.
Por ultimo vimos la inversa de una
matriz que es muy distinto a la matriz original, la regla de Cramer la adjunta
de una matriz, donde en todas seguían siendo matrices solo lo que cambiaba el método
para resolverlo.
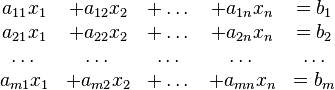
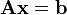
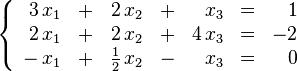


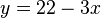
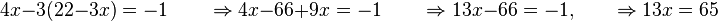
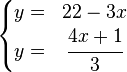


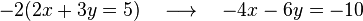

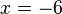
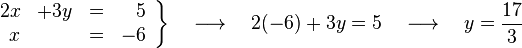

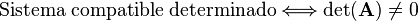



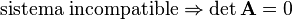



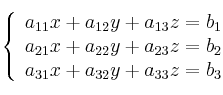
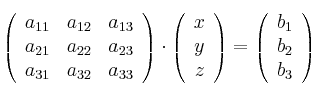
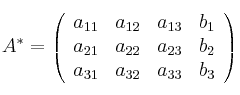












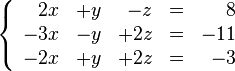


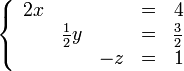

![\left [
\begin{array}{rrrr}
2 & 1 & -1 & 8 \\
-3 & -1 & 2 & -11 \\
-2 & 1 & 2 & -3
\end{array}
\right ]](https://upload.wikimedia.org/math/b/7/5/b75b0e02a527cf69e6f42dbd2fe2960f.png)
![\left [
\begin{array}{rrrr}
2 & 0 & 0 & 4 \\
0 & 1/2 & 0 & 3/2 \\
0 & 0 & -1 & 1
\end{array}
\right ]](https://upload.wikimedia.org/math/e/b/f/ebf74f6593b310153d2a6700d2f37b43.png)
![\left [
\begin{array}{rrrr}
1 & 0 & 0 & 2 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & -1
\end{array}
\right ]](https://upload.wikimedia.org/math/d/4/0/d40cfce339ef9bb6dde8739c55d238d3.png)
![\left [ \begin{array}{cccc}
0 & 0 & 0 & a \\
\end{array} \right ]](https://upload.wikimedia.org/math/4/e/a/4ea82b742b346fc121881fd94c0d3d0c.png)
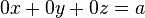 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 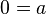 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.