Modulo 2. Integración.

 Matemáticas II

 

Objetivo General:

El estudiante adquirirá destreza en el manejo de técnicas y procedimientos para la solución de problemas. Hará uso de lenguaje matemático, de la sistematización de información y de las formas de representación gráfica  y analítica.

Manejará los conocimientos, métodos y algoritmos matemáticos establecidos en los programas, tanto básicos como auxiliares para abordar los contenidos de otras materias. Elaborará y usará modelos matemáticos en la resolución de problemas de optimización de recursos y en el análisis económico de problemas en el ámbito de las empresas. 

Modulo 2. Integración. 

Objetivo:

El alumno entenderá el concepto de integral y su relación con la derivada. resolverá problemas de aplicación dando énfasis a aquellos relacionados con las áreas     económico- administrativas tales como: Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.

1.1 Antiderivada.

La anti derivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.

Por ejemplo:


Si f(x) = 3×2, entonces, F(x) = x3, es una anti derivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra anti derivada de f(x).


La anti derivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.


Notación


La notación que emplearemos para referirnos a una anti derivada es la siguiente:





Teorema


Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.






Conclusión: Si g(x) es una anti derivada de f en un conjunto D de números reales, entonces cualquier anti derivada de f es en ese conjunto D se puede escribir comoc constante real.


Fórmula que relaciona la integral definida y la indefinida





http://manasorey1.blogspot.mx/2014/11/21-antiderivada.html

marla nayeli sotelo reyes . (2014). matematicas II. 2015, de andrea Sitio web: http://manasorey1.blogspot.mx/2014/11/21-antiderivada.html

 Julio Profe. (2010). Problema 1 con Antiderivadas . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=HOZtqR0R7Vw

2.2 Integral indefinida.

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.


Se representa por ∫ f(x) dx.


Se lee: integral de x diferencial de x.


∫ es el signo de integración.


f(x) es el integrando o función a integrar.


dx es diferencial de x, e indica cuál es la variable de la función que se integra.


C es la constante de integración y puede tomar cualquier valor numérico real.


Si F(x) es una primitiva de f(x) se tiene que:


∫ f(x) dx = F(x) + C


Para comprobar que la primitiva de una función es correcta basta con derivar.



Ejemplo:




Sustitición:




u= 4x-3
du= 4
dx
du= 4x dx







https://sites.google.com/site/cicmolinahelvira/unidad-ii-integral-indefinida-y-metodos-de-integracion/2-1-dfinicion-de-integral-indefinida

CIC_MolinaH.Elvira. (2014). ๋ Unidad II. Integral indefinida y métodos de integración‎ . 2015, de andrea Sitio web: https://sites.google.com/site/cicmolinahelvira/unidad-ii-integral-indefinida-y-metodos-de-integracion/2-1-dfinicion-de-integral-indefinida

2.2.1 Integración con condiciones iniciales.

Hemos dicho que la ecuación y =∫f(x)dx admite infinitas soluciones que difieren en una constante.


Esto significa que las gráficas de dos primitivas cualesquiera de f son traslaciones verticales una de la otra.


Por ejemplo, en la figura de la izquierda mostramos varias gráficas de primitivas de la forma:


y = 2 3 ∫(3x −1)dx = − x x + C


(solución general) para diversos valores enteros de C.


Cada una de esas primitivas es una solución de la ecuación


dy 2 dx = 3x −1


Una solución particular de esta ecuación será una única primitiva, es decir, conocemos el valor de la constante C.


En muchas aplicaciones de la integración, hay información suficiente como para conocer este valor particular de C.


Esta información se llama condición inicial (que abreviamos como c.i.), nombre debido al hecho que en las aplicaciones, generalmente la variable independiente es el tiempo t.


Por ejemplo, en el caso anterior, una c.i. sería que la curva debe pasar por el punto (2, 4). Para hallar esta curva en particular, usamos la información:


F(x) = x3 – x +C (solución general) F(2) = 4 (condición inicial) Resulta que C = -2, como puede deducirse fácilmente.


http://www.cfm.cl/~rjimenez/bioingenieria/cap4.pdf

Prof. Dr. Raúl F Jiménez. (2014). CÁLCULO INTEGRAL. 2015, de andrea Sitio web: http://www.cfm.cl/~rjimenez/bioingenieria/cap4.pdf

2.3 Formulas básicas de integración.


La integración es fundamental en las matemáticas avanzadas especializadas en los campos del cálculo. Una integral es una ANTIDERIVADA, es decir, la operación inversa a la derivada.


Formulas básicas de integración.


Recordemos que como en las derivadas, las integrales poseen reglas, propiedades y formulas para su procedimiento. Las integrales poseen un signo en su inicio en forma de S alargada y con una terminación de dx, esto las diferencia de otras ecuaciones. Una integral a realizar siempre ira acompañada de una S alargada al inicio y un dx al final. Estas son las formulas básicas de integración.







La integral de “n” numero siempre será nx + C. Ejemplo











La integral de una constante siempre será constante * variable +C (ax+C)







La integral de X elevado a “n” numero será Xn+1, lo que se haga en la exponenciación de la X se pondrá también abajo dividiéndola, es una regla establecida. Ejemplo












La integral que divide arriba sobre una variable abajo será logaritmo natural de variable mas C. La formula marca lnX+C porque arriba en dx no tiene constante ni variable pero sí un 1 imaginario, ejemplo.












La integral de un producto se puede separar siempre y cuando no se altere su ecuación. De esta forma se integra en partes. No tienen que ser 3 productos necesariamente para usar la formula ;) Ejemplo.











La integral de un Binomio (V) es parecida a la formula 3, solo que acá al sacar la derivada del binomio (dv) se comprueba que exista la derivada fuera de V, en caso que no exista, se iguala hasta quedar exacto y se elimina, quedando solo el binomio (V) mas la exponenciación + 1.







Se saca el binomio que es (2+X2)


La derivada del binomio es 2X y se le agrega dx, queda 2Xdx. Se comprueba que 2X coincida con el producto de afuera que es X, como es 2X y tenemos X solamente, entonces se tiene que igualar a 2X…¿Cómo?, multiplicando 2(X), lo que hagamos dentro se hace afuera pero en reciproco. Y se elimina la igualdad quedando lo restante.







Ya que se elimino el producto de afuera, se procede con la formula 3, y el ½ estará multiplicando al resultado que quede de la formula.







El 2 que esta en la división del binomio tiene que desaparecer, no se puede multiplicar directo con el 2 de afuera. Para eliminarlo se debe multiplicar medios con medios, extremos con extremos.







https://ingenieriaensistemasuat.wordpress.com/2010/12/14/381/

Ingenieria en Sistemas de UAT Matamoros. (2010). Introducción a las Formulas básicas de Integración.. 2015, de andrea Sitio web: https://ingenieriaensistemasuat.wordpress.com/2010/12/14/381/

UTTAB. (2011). Formulas basicas de integracion . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=BVF1Xa7wBC8

2.3.1 integral indefinida de una constante.

Llamamos al conjunto de todas antiderivadas de una función la integral indefinida de la función. Escribimos la integral indefinida de la función f como



f(x) dx y la leemos como "la integral indefinida de f(x) respecto a x" Por lo tanto,



f(x) dx es una conjunto de funciones; no es una función sola, ni un número. La función f que se está integrando se llama el integrando, y la variable x se llama la variable de integración.


Ejemplos:

2x dx = x2 + C

La intgegral indefinida de 2x respecto a x es x2 + C


4x3 dx = x4 + C


La integral indefinida de 4x3 respecto a x es x4 + C


Leyendo la formula


Leemos la primera formula más arriba como sigue:


2xdx=x2 + C


La antiderivadade 2x,respecto a x,es igual a x2 + C


La constante de integración, C, nos recuerda que podemos añadir cualquiera constante y así obtener una otra antiderivada.



http://www.zweigmedia.com/MundoReal/tutorials4/frames6_1.html

Stefan Waner. (2008). La integral indefinida. 2015, de andrea Sitio web: http://www.zweigmedia.com/MundoReal/tutorials4/frames6_1.html

2.3.2 Integral de una constante por una variable.

es el conjunto de las infinitas primitivas que puede tener una función.


Se representa por ∫ f(x) dx.


Se lee : integral de f de x diferencial de x.


∫ es el signo de integración.


f(x) es el integrando o función a integrar.


dx es diferencial de x, e indica cuál es la variable de la función que se integra.


C es la constante de integración y puede tomar cualquier valor numérico real.


Si F(x) es una primitiva de f(x) se tiene que:


∫ f(x) dx = F(x) + C


Para comprobar que la primitiva de una función es correcta basta con derivar.


Propiedades de la integral indefinida


1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.


∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx


2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.


∫ k f(x) dx = k ∫f(x) dx


http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

@vitutor 2014. (2014). Integral indefinida. 2015, de andrea Sitio web: http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

https://www.youtube.com/watch?v=l6IRgULsAdM

Janet Lopez. (2012). Derivada de una constante por una variable . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=l6IRgULsAdM

2.3.3 Integral de xn.

Potencia de x.



xn dx = x(n+1) / (n+1) + C (n -1)




demostración Desde la Derivada


Dando :
x^m = m x^(m-1)
El Teorema Fundamental de Cálculo


m x^(m-1) dx = x^m dx = x^m + d. (El Teorema Fundamental de Cálculo (d = una constante arbitraria)


x^(m-1) dx = x^m / m + c (Divida ambos lados por m) (c=una constante arbitraria, d/m = c)


x^n dx = x^(n+1) / (n+1) + c (Fije m=n+1, substitución) QED.


http://aprendematematicas2.blogspot.mx/2015/11/233-integral-de-xn.html

karenh. (2015). matematicas 2. 2015, de andrea Sitio web: http://aprendematematicas2.blogspot.mx/2015/11/233-integral-de-xn.html

2.3.4 Integral de en.


ex dx = ex + C




e^x dx : Desde la derivada





Dado : e^x = e^x. Teorema Fundamental de Cálculo





e^x = e^x




e^x dx = e^x + c (constante C)




http://aprendematematicas2.blogspot.mx/2015/11/234-integral-de-en.html

karenh. (2015). matematicas 2. 2015, de andrea Sitio web: http://aprendematematicas2.blogspot.mx/2015/11/233-integral-de-xn.html

2.3.5 Integral de una constante por una función de x.

Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).


Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:


F'(x) = f(x).


Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.


[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)


http://aprendematematicas2.blogspot.mx/2015/11/235-integral-de-una-constate-por-una.html

karenh. (2015). matematicas 2. 2015, de andrea Sitio web: http://aprendematematicas2.blogspot.mx/2015/11/233-integral-de-xn.html

2.3.6 Integral de una suma (diferiencia) de funciones.

Se puede mostrar la suma de los numeros integrales en la linea numerica mueve a la derecha por los numeros positivos y a la izquierda por negativos.


Ejemplo:


(+5) + (-3)



Paso 1:

Comienza en el 0 y mueve 5 unidades en la linea numerica a la derecha por lo de (+5)







Ahora sumar (-3) significa regresarte en la linea numerica.



Paso 2:

Comienza en el +5 y mueve a la izquierda 3 unidades por eso del (-3) y quedas en la linea de +2









La linea numerica muestra que (+5) + (-3) = +2.


Usa la siguiente regla para sumar integrales.



Regla 1

Si los integrales son del mismo signo, suma los numeros y conserva el mismo signo

(+2) + (+4) = +6(-2) + (-4) = -6



Regla 2

Si los integrales tienen diferente signo, resta los numeros sin tomar en cuenta el signo y da al resultado el signo del numero mas grande

(-4) + (+2) = -2


4 - 2 = 2 y como el 4 es negativo y es el numero mas grande el resultado es negativo,igual a -2.


Par sumar mas de 2 integrales encuentra la suma de todos los numeros positivos, despues la suma de los negativos y luego utiliza la regla 2, que es restar y dar al resultado el signo del numero mayor.





http://aprendematematicas2.blogspot.mx/2015/11/236-integral-de-una-suma-diferencia-de.html

karenh. (2015). matematicas 2. 2015, de andrea Sitio web: http://aprendematematicas2.blogspot.mx/2015/11/233-integral-de-xn.html

2.3.7 Regla de potencias.

Regla de potencias


Para cualquier numero real n.



d/dx xn = nxn-1


DEMOSTRACIÓN:


EJEMPLO REGLA DE LAS POTENCIAS:


Diferencie.


a) Y = x7


b) Y = x


c) Y=x-2/3


d) Y=x raiz de 2


Solución por las reglas de las potencias.


a) Con n = 7; dy/dx = 7x7-1= 7x6,


b) Con n = 1; dy/dx = 1x1-1 = x0 = 1,


c) Con n = 2/3: dy/dx= (-2/3)x(-2/3)-1 = -2/3x-5/3= -2/3x5/3’












http://calculoumgsanmarcos.ccvsanmarcos.com/b-regla-de-potencias-y-sumas/

WordPress. (2015). B. REGLA DE POTENCIAS Y SUMAS. 2015, de andrea Sitio web: http://calculoumgsanmarcos.ccvsanmarcos.com/b-regla-de-potencias-y-sumas/

https://www.youtube.com/watch?v=6TWPRp8txwA

profmena. (2013). REGLA DE LA POTENCIA (Ejemplos ilustrativos) . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=6TWPRp8txwA

2.3.7.1 Integrales que incluyen un trinomio cuadrado perfecto.


Son aquellas integrales que tienen funciones trigonométricas elevadas a exponentes. Para su mejor comprensión se ha separado en diferentes casos.



Caso 1


Integrales de la forma








Identidad trigonométrica


cos2 x + sen2 x =1


Protocolo a seguir












http://www.calculointegrales.com/p/integrales-trigonometricas.html

PAULA BUSTOS. (2014). Cálculo de integrales. 2015, de andrea Sitio web: http://www.calculointegrales.com/p/integrales-trigonometricas.html

https://www.youtube.com/watch?v=Ur23w3GQhKc

 Sergio Esteves Rebollo. (2013). Integrales - Identificación por Trinomio Cuadrado Perfecto . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=Ur23w3GQhKc

2.3.7.2 integrales que incluyen funciones exponenciales.

Para valores reales de x, la integral exponencial Ei(x) se define como




Esta definición puede ser utilizada para valores positivos de x, pero a causa de la singularidad del integrando en cero, la integral debe ser interpretada en término del valor principal de Cauchy. Para valores complejos del argumento, esta definición es ambigua a causa de los puntos de ramificación en 0 y en .1En general, se realiza un corte en el eje real negativo y Ei puede ser definida mediante una continuación analítica en el resto del plano complejo.


Se utiliza la siguiente notación,2




Para valores positivos de la parte real de , esto se puede expresar como3




El comportamiento de E1 cerca del branch cut puede ser analizado mediante la siguiente relación:4



https://es.wikipedia.org/wiki/Integral_exponencial

Fundación Wikimedia, Inc.. (2014). Integral exponencial. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Integral_exponencial

2.3.8 Integrales que incluyen funciones logarítmicas.

http://martinlimon3105.blogspot.mx/2015/11/238-integrales-que-incluyen-funciones.html

Martin Limon . (2015). Integrales que incluyen funciones logarítmicas.. 2015, de andrea Sitio web: http://martinlimon3105.blogspot.mx/2015/11/238-integrales-que-incluyen-funciones.html

 professor.ingeniero. (2013). INTEGRAL LOGARITMO ejemplos resueltos . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=W5lYU9k5Y4Q

2.3.9 Integrales que incluyen (1/u)du.

http://matematicas2jairoreyes.blogspot.mx/2014/11/239-integrales-que-incluyen-1u-du.html

Matemáticas II. (2014). Integrales que incluyen (1/u) du. 2015, de andrea Sitio web: http://matematicas2jairoreyes.blogspot.mx/2014/11/239-integrales-que-incluyen-1u-du.html

2.3.10 integrales incluyen au.

http://martinlimon3105.blogspot.mx/2015/11/2310-integrales-incluyen-au.html

Martin Limon . (2015). Integrales incluyen au. 2015, de andrea Sitio web: http://martinlimon3105.blogspot.mx/2015/11/2310-integrales-incluyen-au.html

2.2.11 Integral por partes.

es el que resulta de aplicar el siguiente teorema:










Regla mnemotécnica: "Un Día Vi Una Vaca Vestida De Uniforme".





Eligiendo adecuadamente los valores de 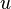y , puede simplificarse mucho la resolución de la integral.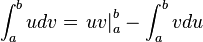




.




Desde un punto de vista didáctico se recomienda escoger la función u de acuerdo con el orden:[cita requerida]
Trigonométrica Inversa
Logarítmica
Algebraica o polinómica
Trigonométrica
Exponencial.


Otra recomendación sería cambiar el orden de trigonométrica y exponencial. Si seguimos esta otra recomendación podemos usar la regla mnemotécnia ALPES, asignándole el puesto de u de acuerdo con el orden de aparición:
Arcoseno(y cualquier trigonométrica inversa)
Logarítmica
Polinómica
Exponencial
Seno/coseno(y cualquier trigonométrica.






https://es.wikipedia.org/wiki/M%C3%A9todos_de_integraci%C3%B3n#M.C3.A9todo_de_integraci.C3.B3n_por_partes

Fundación Wikimedia, Inc.,. (2015). Métodos de integración. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/M%C3%A9todos_de_integraci%C3%B3n#M.C3.A9todo_de_integraci.C3.B3n_por_partes

 

Julioprofenet. (2011). Integración por Partes - Ejercicio 2 . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=BETtnGGLATU

2.4 aplicaciones: determinación de funciones de costo, utilidades, consumo y ahorro a partir de sus marginales.

DETERMINACIÓN DE FUNCIONES DE COSTO:
Servir de base para fijar precios de venta y para establecer políticas de comercialización.
Facilitar la toma de decisiones.
Permitir la valuación de inventarios.

Controlar la eficiencia de las operaciones

UTILIDADES:
Utilidad es la propiedad por la cual una cosa o acción adquiere la condición de valor útil para satisfacer las necesidades humanas. Puede hacer referencia a los siguientes términos:
 En economía: utilidad (economía) a la función de utilidad, cuya derivada es la utilidad marginal; a un criterio para encontrar el punto óptimo de eficiencia de Pareto, en el cual no es posible beneficiar a más elementos de un sistema sin perjudicar a otros; y a la subjetividad de la utilidad esperada; En filosofía: al utilitarismo, una teoría ética.
 En informática: a una herramienta que sirve de soporte para la construcción y ejecución de programas;
En el derecho registral: al catálogo de montes de utilidad pública; al monte de utilidad pública;
En contabilidad también denominado beneficio, es la diferencia entre los ingresos obtenidos por un negocio y todos los gastos incurridos en la generación de dichos ingresos; véase beneficio económico

CONSUMO Y AHORRO A PARTIR DE SUS MARGINALES.
La propensión marginal al consumo mide el incremento que se produce en el consumo cuando la renta crece en una unidad. Teniendo en cuenta que los crecimientos de la renta se destinan parcialmente a un mayor consumo y parcialmente a un mayor ahorro, la propensión marginal se sitúa entre cero y uno.
La función de consumo agregado puede escribirse de la siguiente forma:
C = a + c x Y
En esta expresión C representa el gasto de consumo, mientras que Y es la renta disponible. Cuando la renta disponible se incrementa, el gasto total de consumo crece en una proporción igual a c, que es la propensión marginal a consumir. El término a de la función de consumo se denomina consumo autónomo, y recoge aquel nivel mínimo de consumo que se realizaría aunque no se dispusiese de renta en un periodo.
Junto al concepto de propensión marginal a consumir se define el concepto de propensión media al consumo, o cociente entre el gasto total en consumo y la renta disponible. Una propiedad de esta función de consumo es que, aunque decreciente, esta propensión media es mayor que la propensión marginal:
C / Y = a/Y + c
La propensión marginal al ahorro (s) es igual a 1-c, ya que las familias destinan al ahorro (S) los incrementos de renta que no destinan al consumo.
Y = C + S
ΔY = ΔC + ΔS
1 = ΔC/ΔY + ΔS/ΔY
1 = c + s


http://www.expansion.com/diccionario-economico/propension-marginal-al-consumo-ahorro.html

Uxó González, Jorge. (2015). PROPENSIÓN MARGINAL AL CONSUMO/AHORRO. 29 Nov. 2015, de expansión Sitio web: http://www.expansion.com/diccionario-economico/propension-marginal-al-consumo-ahorro.html

En este segundo módulo vimos que eran las antiderivas donde pueden ser exponenciales, logarítmicas, de fracción, multiplicación de ecuaciones; pero para resolverlas todos tienen que cumplir con ciertos pasos; aunque depende la operación se incluye algunos diferentes.

Y la integración por partes que es un poco complicada porque la fórmula de dice que tienes que determinar que parte de la ecuación derivar primero; pero algunas de fracción y logaritmo son un poco más complicadas; además de que estos ejercicios son largos y si te equivocas en un numero todo el ejercicio está mal.

Y  tienes que saber realizar algunas operaciones de fracciones porque tienes que ir simplificando el resultado.

Jagdish C. Arya. (2009). Matemáticas aplicadas a la administración y a la economía. cuarta edición. México: PEARSON EDUCACION.