MODULO 3. INTEGRAL DEFINIDA.
Objetivo.
El alumno comprenderá el concepto de integral definida así como si interpretación gráfica. resolverá problemas de aplicación geométrica al mismo tiempo que resolverá problemas del entorno económico-administrativo.
El alumno aplicara técnicas adicionales para la resolución de integrales que presentan estructuras complejas asociadas con modelos y problemas del entorno económico-administrativo.
El alumno entenderá los conceptos elementales del álgebra lineal y los aplicara en problemas del ámbito económico y de gestión de negocios.
3.1 Área bajo la curva.
Enseguida, graficaremos una función en un intervalo [a,b] y se mostrará el área contenida entre su gráfica y el eje x en el intervalo dado. Observa la siguiente gráfica.
 |
Igual que con el problema de la tangente, empezaremos por hacer aproximaciones. Aproximaremos el área bajo la curva con el área de ciertos rectángulos.
Observa las siguientes gráficas:
 |
 |
Como pudiste ver en las gráficas anteriores, con los primeros rectángulos estamos sobreestimando el valor del área y con los segundos rectángulos la estamos subestimando.
A continuación calcularemos aproximaciones cada vez mejores, tomando cada vez más y más rectángulos.
Observa las siguientes animaciones.
 |
 |
El valor exacto del área es:
136
| |||
Área =
|
aprox. igual
|
45.3333
| |
3
|
Los resultados anteriores parecen indicar que conforme el número n de rectángulos crece, (n---> ), el valor del área de los rectángulos tanto por la izquierda como por la derecha se acercan a un mismo número. Vamos a cuantificar y a formalizar las ideas expuestas anteriormente.
), el valor del área de los rectángulos tanto por la izquierda como por la derecha se acercan a un mismo número. Vamos a cuantificar y a formalizar las ideas expuestas anteriormente.
Dada una función f(x)>0 en un intervalo [a,b], para encontrar el área bajo la curva procedemos como sigue:
| ||||||
Para ejemplificar lo anterior, ahora se calculará la suma de Riemann como función de n, el número de rectángulos. También se calculará el límite cuando n--> , cuyo valor es, por definición, el área bajo la curva.
, cuyo valor es, por definición, el área bajo la curva.
f(x)= x2 + 1
Si escogemos el extremo derecho de los subíntervalos, tendríamos que
Desarrollando la expresión anterior, nos queda:

http://centros5.pntic.mec.es/ies.de.melilla/area_bajo_curva.htm
2.1.2 El área bajo una curva. (2014). El área bajo una curva. 2015, de andrea Sitio web: http://centros5.pntic.mec.es/ies.de.melilla/area_bajo_curva.htm Matefis. (2013). Area bajo la curva I (integral definida) . noviembre 30, 2015, de YouTUbe Sitio web: https://www.youtube.com/watch?v=yc4ERt8aiQA 3.2 teorema fundamental del calculo.Dada una función f integrable sobre el intervalo 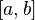 , definimos F sobre , definimos F sobre 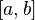 por por 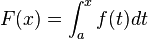 . Si f es continua en . Si f es continua en  , entonces F es derivable en , entonces F es derivable en  y F'(c) = f(c). y F'(c) = f(c). Usando la Regla de la cadena obtenemos como consecuencia directa del primer teorema fundamental del cálculo infinitesimal:  Siendo f(t) una función integrable sobre el intervalo [a(x),b(x)] con a(x) y b(x) derivables. Demostración[editar] Lema[editar] Sea  integrable sobre integrable sobre 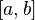 y y Entonces  Demostración del lema[editar] Está claro que 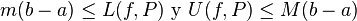 para toda partición para toda partición  . Puesto que . Puesto que  , la desigualdad se sigue inmediatamente. , la desigualdad se sigue inmediatamente.Demostración[editar] Por definición se tiene que  . .Sea h>0. Entonces 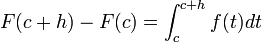 . .Se define 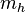 y y 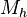 como: como: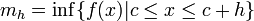 , ,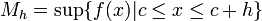 Aplicando el 'lema' se observa que  . .Por lo tanto,  Sea 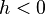 . Sean . Sean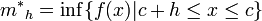 , ,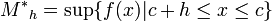 . .Aplicando el 'lema' se observa que  . .Como 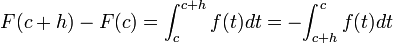 , ,entonces,  . .Puesto que 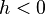 , se tiene que , se tiene que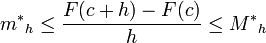 . .Y como  es continua en c se tiene que es continua en c se tiene que , ,y esto lleva a que 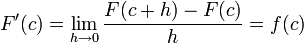 . .Ejemplos[editar]    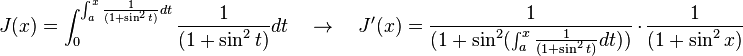 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fundación Wikimedia, Inc.. (2015). Teorema fundamental del cálculo. 2015, de andrea Sitio web: https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo#Primer_teorema_fundamental_del_c.C3.A1lculo
Julio Profe. (2012). Teorema Fundamental del Cálculo . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=SCKpUCax5ss
3.3 propiedades de la integral definida.
1. El valor de la integral definida cambia de signo si se permutan los límites de integración.

2. Si los límites que integración coinciden, la integral definida vale cero.

3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

4. La integral definida de una suma de funciones es igual a la suma de integrales·

5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

http://www.vitutor.com/integrales/definidas/integral_definida.html
@vitutor 2014. (2014). Integral definida. 2015, de andrea Sitio web: http://www.vitutor.com/integrales/definidas/integral_definida.html
https://www.youtube.com/watch?v=L4K4JXMXJbI
Tareas Plus. (2012). Integral definida y sus propiedades básicas . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=L4K4JXMXJbI
3.4 Área entre una y dos curvas.
En esta sección estudiaremos como calcular el área entre dos curvas.
El problema es el siguiente: Dadas dos funciones f y g , encontrar el área contenida entre sus gráficas en el intervalo [a,b] .
Para ilustrar el problema y el procedimiento, observa el siguiente ejemplo.
f(x)= 3x3 - x2 - 10x
|
g(x)= - x2 + 2x
|
 |  |
 | |
Utilizaremos el mismo procedimiento que se usó para encontrar el área bajo una curva. Se aproximará el área entre las dos curvas haciendo una partición del intervalo [a,b] en n subintervalos de longitud(b-a)/n. En cada subintervalo escogemos un valor particular de x, al que llamaremos x*.
|
En cualquier caso la altura de los rectángulos es |f-g| (valor absoluto de la diferencia).
|
Enseguida se calculará el área de la región entre dos curvas.
| Dentro del intervalo (-2,2), las curvas: y=2(1-x2) y y=x2-1 se intersectan en x = -1, 1. f(x)=2(1 - x2) ; g(x)=x2-1 El área entre las curvas en cada subintervalo es: {4, 4, 4}Cada una de estas áreas tiene que ser calculada por separado. El área total entre las curvas es: 4 + 4 + 4 = 12 |  |
| Dentro del intervalo (-1,1.5), las curvas: y = -x2/3+1 y y = x2/3 se intersectan en x = 1. f(x)= -x2/3+1 ; g(x)=x2/3-1El área entre las curvas en cada subintervalo es: {1.6, 0.15867} Cada una de estas áreas tiene que ser calculada por separado. El área total entre las curvas es:1.6 + 0.15867 = 1.75867 |  |
2.3.3 El área entre dos curvas. (2014). 2.3.3 El área entre dos curvas. 2015, de andrea Sitio web: http://centros5.pntic.mec.es/ies.de.melilla/area_entre_dosC.htm
ibelloj. (2011). Área entre dos curvas . noviembre 30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=ljWj8QgQAa4
3.5 aplicaciones: Excedente del consumidor y del productor, valor presente y valor futuro.
Excedente del consumidor
Podemos definir el excedente del consumidor como la diferencia entre el precio máximo que estaría dispuesto a pagar y el precio que realmente paga. Consideremos la siguiente curva de demanda de un individuo, si el precio de mercado es pE demandara qE. No obstante, por la primera unidad hubiera estado dispuesto a pagar mucho más p1 , por la segunda unidad algo menos que por la primera pero más de lo que realmente paga, y así sucesivamente hasta la cantidad qE en donde coincide el precio que paga y el que está dispuesto a pagar. Gráficamente, la zona que muestra la divergencia entre la disposición marginal a pagar y el precio satisfecho reflejaría el excedente del consumidor.Excedente del productor
Para estimar el excedente del productor deberemos de partir de la función de oferta. Dado un precio en el mercado pE, compararemos el precio al que estarían dispuesto a ofrecer cada unidad de mercancía con el precio que realmente perciben. Y observaremos que hasta qE el empresario por cada unidad ofrecida recibe un precio superior al que estaría dispuesto a percibir. Dicha zona delimita gráficamente el excedente del productor.Academatica. (2013). excedente del consumidor y productor - ejemplo 1 . noviembre30, 2015, de YouTube Sitio web: https://www.youtube.com/watch?v=rWzUkjlwmyo
Jagdish C. Arya. (2009). Matemáticas aplicadas a la administración y a la economía. cuarta edición. México: PEARSON EDUCACION.
En este tercer módulo vimos áreas de
integrales donde realizábamos las gráficas para demostrar el área que tomaba
esa ecuación; el área de regiones entre dos curvas donde te daban dos
ecuaciones en las cuales tenías que demostrar por cuanto espacio estaba ocupador
estas.
Así como las integrales impropias
donde el resultado es infinito, que estas eran de las más sencillas que
realizamos, y en estas tiene que venir definido de que distancias se desarrolla.
Estos temas los vimos muy rápido pero
entendimos, solo que se nos dificulta al momento de ver que son logaritmos.


No hay comentarios:
Publicar un comentario